
动画按钮的使用2
例3 作一个四个端点可以在屏幕上任意运动的四边形,然后作它的中点四边形,观察中点四边形是什么四边形。
[简要步骤]:
(1)用画点工具作点A、B、C、D,连接AB、BC、CD、AD,然后选中点A、B、C、D,打开编辑菜单,作“动画”按钮,如图2.3;
(2)选中线段AB、BC、CD、AD,利用作图菜单的中点命令,作出各边的中点,连接中点,作出中点四边形EFGH,如图2.4;
(3)利用度量菜单度量线段EF、FG、GH、EH的长度,以及它们的斜率,如图2.5。
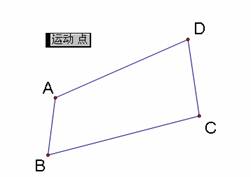
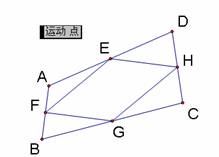
图2.3 图2.4

图2.5
单击“运动”按钮,观察A、B、C、D的运动方式,以及中点四边形各边的长短和斜率的变化情况。注意此时A、B、C、D四点是在屏幕上任取的四点,所以它们的运动路径就是整个平面,在平面上作随机运动。
例4 任作两条线段AB、CD,并在这两条线段上各取一点E、F,连接EF,求线段EF中点G的轨迹。
分析:本例中E、F点分别在线段AB、CD上运动,因此可以构造多点的动画,跟踪中点G,观察G的轨迹。由于线段AB、CD的长短、垂直、平行等情况的不同,线段中点G的轨迹将呈现多样性。如图2.6所示。
由于点G是由两个自由点E、F所控制,因此无法直接作出点G的轨迹。我们可以先固定点E,画出点G关于点F的轨迹(一条线段),然后利用作图菜单中的“轨迹”,得到此线段关于点E的轨迹。
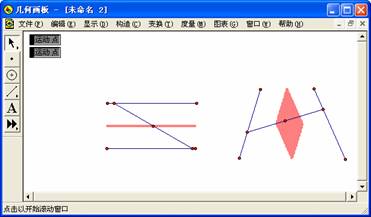
图2.6
[简要步骤]:
(1)在绘图窗口中任作两条线段AB、CD,并在线段AB、CD上分别取点E、F;
(2)连接EF,作线段EF的中点G,并跟踪点G;
(3)依次选中点E、点F,利用编辑菜单中“操作类按钮”,选“动画”、并将动画速度都改为“中速”,然后确认,得到动画按钮。
单击动画按钮,便可看到点G的轨迹。我们可以用以下作法,作出点G的轨迹。
(4)连接EC、ED,分别作出线段EC、ED的中点H、I,连接HI;
(5)选中线段HI和点E,利用构造菜单中的“轨迹”,得到线段HI关于点E的轨迹,即点G关于点E、F的轨迹。
不妨改变线段AB或线段CD的长短或方向,观察点G的轨迹发生什么变化。
动画按钮的使用2
分析:本例也是多点动画,我们假设月亮绕地球转、地球绕太阳转的轨道都为圆。当地球绕着太阳转,同时月亮着地球转的时候,可以发现月亮绕地球转动的轨道也在绕着太阳转。
(1)在绘图窗口中任作四条线段AB、CD、EF、GH,分别表示太阳、地球、月亮的半径、月亮绕地球运动的轨道;
(2)以任意点I为圆心,AB为半径,作代表太阳的圆,作出圆的内部,并将颜色变为红色;以点I为圆心,作表示地球绕太阳转的轨道的圆IJ,在轨道上任取一点K,以点K为圆心,CD为半径,作代表地球的圆,作出圆的内部,并将颜色变为蓝色;
(3)以点K为圆心,GH为半径,作表示月亮绕地球转的轨道的圆KL,在轨道上任取一点L,以点L为圆心,EF为半径,作代表月亮的圆,作出圆的内部,并将颜色变为黄色;
(4)依次选中点K、点L作动画按钮,使点K转动的速度为慢速,点L转动的速度为快速,如图2.7所示;
(5)隐藏线段AB、CD、EF、GH,点I、J、K、L,圆IJ、KL,单击动画按钮,便可看到地球绕着太阳转,同时月亮绕着地球转。
注意:从上面的例子中我们可以看出,点运动的路径是与点本身的属性有关的。我们可以把几何画板中的点分成三类:一类是自由点,它没有父对象,即可以不受任何限制地在平面上到处移动的点;一类是半自由点,可以在一定的路径内移动的点,如线段和圆上的点,点的父对象就是线段或圆;还有一类是非自由点,由其它几何对象产生,如直线和直线的交点,直线和圆的交点等,如果它要运动,则产生它的父对象都要运动。
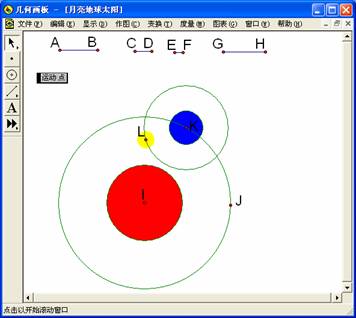
图2.7