
本讲导学
本节介绍了变换菜单的“平移”和“反射”命令的用法。“平移”命令提供了九种平移方式,特别是按“标记向量”平移是最常用的一种方式,需要熟练掌握。“反射”则十分简单,通过简单的练习即能掌握。
几何画板中,平移可以按三大类九种方法来进行,其中有些方法事先要标记角、标记距离或标记向量。(变换都提供了预览的功能,这样可以事先发现我们的结果是不是我们想要的)
选中要作平移的几何对象,打开“变换”菜单的“平移”命令,则出现如图3.1所示的对话框,此时你可以选择按照“极坐标”方式、“直角坐标”方式或“标记”方式平移。其中“标记”方式只有当标记了一个向量时,才可用。然后输入平移的距离或角度,“标记距离”或“标记角度”需要事先标记一个距离或角度以后才可用。

图3.1
在极坐标系中最多可以组合出四种方法,如图3.2所示:

图3.2
在直角坐标系中最多可以组合出四种方法,如图3.3所示:

图3.3
按标记的向量平移有一种方法,此时角度和方向都指定,如图3.4所示:

图3.4
即我们一共有9种方法实现对象的平移。
二、典型例题
分析:根据勾股定理,让一个点在直角坐标系中按水平方向、垂直方向都平移1cm,得到的点与原来的点总是相距 cm,然后以圆心和圆周上的点画圆即可。
cm,然后以圆心和圆周上的点画圆即可。
[简要步骤]:
(1)画一个点A;
(2)单击点A,选择【变换】|【平移】命令, 在弹出的对话框中作如图3.5的设置:
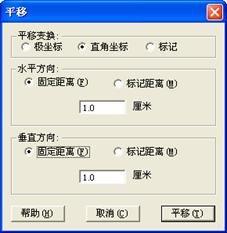
图3.5
(3)顺次单击点A和点A’,选择“作图”菜单的“以圆心和圆周上的点绘圆”命令,最后得到一个圆,无论如何移动,圆的半径固定为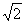 cm。
cm。
[简要步骤]:
(1)画三角形ABC;
(2)另画一条水平线段DE;
(3)在线段上画一点F;
(4)选中点D、F,选择“变换”菜单的“标记向量”命令;
(5)选中三角形ABC,然后选择“变换”菜单的“平移”命令,如图3.6。
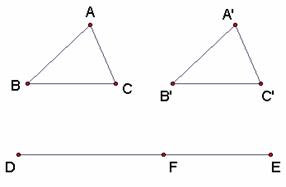
图3.6
拖动点F在线段DE上移动,可演示两个三角形重合和分开,可用来说明全等形。
[简要步骤]:
(1)在绘图窗口中作三条交于一点的线段AB、AC、AD;
(2)选点A、B、C和线段AB、AC,利用变换菜单的“平移”命令,在对话框内(参见图3.7(a))选“直角坐标”,在水平方向填入3,垂直方向填入0,得到点A¢、B¢、C¢ 和线段A¢B¢、A¢C¢;
(3)选点A、B,利用变换菜单的“标识向量”命令,标识向量AB;
(4)选线段A¢C¢ 和端点C¢,利用变换菜单的“平移”命令,在对话框内(参见图3.7(b))选“标记”平移得到线段B¢D¢,连接C¢D¢,得到平行四边形A¢B¢D¢C¢;
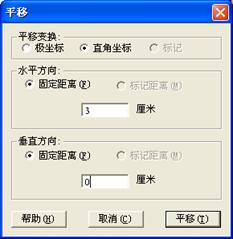
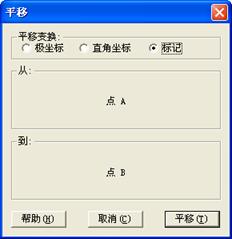 ??
??
(a) (b)
图3.7
(5)选点A、D,利用变换菜单的“标识向量”命令,标识向量AD;
(6)选中整个平行四边形A¢B¢D¢C¢,利用变换菜单的“平移”命令,在对话框内选“根据标识的向量”平移得到平行四边形A¢¢B¢¢D¢¢C¢¢,连接线段A¢A¢¢、B¢B¢¢、D¢D¢¢和C¢C¢¢,并将线段A¢C¢、C¢C¢¢、C¢D¢ 改为虚线,即得到所需的平行六面体A¢¢B¢¢D¢¢C¢¢-A¢B¢D¢C¢,如图3.8所示;
(7)分别拖动点B、D、C,或它们的组合,观察平行六面体A¢¢B¢¢D¢¢C¢¢-A¢B¢D¢C¢ 的变化情况。

图3.8
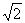 cm的圆。
cm的圆。