
本节导学
本节介绍了如何利用“轨迹”命令画函数以及参数方程的图像。利用轨迹命令可以画一些利用“图表”菜单不能作出的函数图像,而且可以更好的控制函数图像的动态变化,在绘制函数图像中十分重要,是本章的重点也是难点。
利用轨迹画函数的一般方法
“作图”菜单中的“轨迹”命令是几何画板的重要功能,利用它不仅能作出各种动态图形的轨迹,而且还能作出各种函数图像。利用“轨迹”功能作出的函数图像,是利用点的动态变化来作图,这样可以通过点的运动来控制函数图像的动态变化,体现特殊的动态效果,这在数学课件制作中是非常有用的功能。
要作出对象的轨迹,要选中两个对象:一个对象叫主动点,它必须在某个运动路径上(可以看作确定一个函数的定义域),例如线段、射线、直线、圆、多边形等;然后是被动对象,即由主动点产生的、与主动点有内在联系的结果对象(可以看作确定函数的对应方式),然后再单击“作图”中的“轨迹”,即可作出轨迹。
[简要步骤]:
(1)显示坐标轴AB,利用图表菜单中“绘制点”命令,在对话框中分别输入6.28(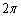 )和0,并确认,得点C(
)和0,并确认,得点C(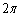 ,0),(也可以利用计算器算得数值
,0),(也可以利用计算器算得数值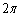 和0,依次选中
和0,依次选中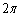 和0,利用图表菜单中“绘制点”,得点C(
和0,利用图表菜单中“绘制点”,得点C(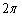 ,0);)连接原点A与C,得线段AC;
,0);)连接原点A与C,得线段AC;
(2)在线段AC上任取一点D(注意在线段AC呈高亮时取点D,这里的点D的横坐标xD满足 ,这一点十分关键),再显示坐标轴AB;
,这一点十分关键),再显示坐标轴AB;
(3)利用度量菜单,度量点D的横坐标。
(4)将角度单位设置成“弧度”状态,利用计算器计算出sin(xD)(注意观察图5.10的计算器示例,留意其中的若干函数,了解其作用是十分有益的);
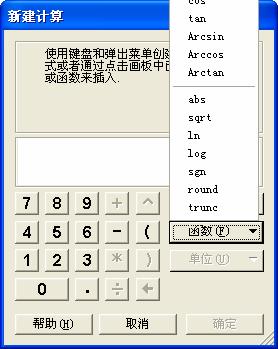
图5.10
(5)依次选取横坐标xD、sin(xD)(注意:切不可颠倒次序),利用图表菜单中“绘制点”,得轨迹点E;
(6)选取主动点D和轨迹点E,利用作图菜单中“轨迹”命令,即得y =sinx,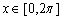 的图像。
的图像。
例2 作函数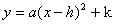 的图像,要求其中a、h、k的大小及其符号能随时改变。
的图像,要求其中a、h、k的大小及其符号能随时改变。 ![]()
[简要步骤]
(1)显示坐标轴,在坐标轴x的负半轴上任取两点C、D,过此两点分别作x轴的垂线;
(2)类似地,在坐标轴y的负半轴上任取一点E,过此点作y轴的垂线;
(3)分别在三条垂线上各取一点F、G、H,并与坐标轴上的点连接成三条线段FC、GD、HE,显示线段的标签,并分别将标签改为a、h、k,隐藏三条垂线;
(4)在x轴上任取一点M,度量点H、M的横坐标和F、G的纵坐标yF、yG,将度量值的标签相应地修改为h、x、a、k;
(5)选中度量a、k、h、x,利用计算器计算出a(x-h)2+k;
(6)依次选中度量x和a(x-h)2+k,利用图表菜单中的“绘制(x,y)”,绘制点P(x,a(x-h)2+k);
(7)选中点P、M,利用作图菜单中“轨迹”,即得图5.11所示的抛物线;
(8)过点G作辅助虚线平行于x轴,过点H作辅助虚线平行于y轴;
(9)隐藏不必要的度量和点线,即得图5.11。

图5.11
拖动点F(上下拖动,以改变a的值),可见抛物线的开口变化;
拖动点G(上下拖动,以改变k的值),可见抛物线的顶点在垂直方向上的变化;
拖动点H(左右拖动,以改变h的值),可见抛物线的顶点在水平方向上的变化。
[简要步骤]
在x轴上画线段CD;
在线段CD上画两点,分别为E、F(F在E的右边);
度量E、F的横坐标;
计算sgn(x -
-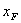 )=-1.00,sgn(
)=-1.00,sgn( =1.00;
=1.00;
再计算( sgn(x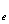 -
-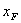 )+1)/2和(sgn(
)+1)/2和(sgn(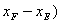 +1)/2;
+1)/2;
计算( sgn(x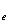 -
- )+1)/2*
)+1)/2*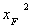 +(sgn(
+(sgn(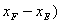 +1)/2[1-(
+1)/2[1-( )];
)];
画点,作轨迹。
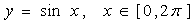 的图像;
的图像;  的图像。
的图像。