
迭代的应用
[简要步骤]:
(1)作一水平直线,作三条与直线垂直的线段AB、CD、EF;
(2)同时选中线段AB、CD,利用“度量”菜单中的“比”得出它们的比值。选中度量值,再选中“变换”菜单的“标记比”,把它标记为缩放的比值。单击“文本工具”,双击度量的比值,在“标签”框中输入“q”;
(3)选中线段EF,度量它的长度,单击“文本工具”,双击度量的长度值,在“标签”框中输入“a”;
(4)选中点“E”,选择“变换”菜单的“平移”命令,在打开的对话框中,在“固定距离”中输入“1”,在“固定角度”中输入“0”,单击“平移”,得到一个点E’。选择点E’,作已知直线的垂线,单击直线与垂线的交点,得点“G”;
(5)双击点G,将它标记为缩放中心,选中点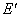 ,选择“变换”菜单的“缩放”命令,选择“标记比”,单击“缩放”,得到点
,选择“变换”菜单的“缩放”命令,选择“标记比”,单击“缩放”,得到点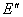 ;
;
(6)隐藏点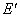 、直线
、直线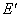 G、线段EF,连接线段
G、线段EF,连接线段 G,,将其“线型”改为“虚线”;
G,,将其“线型”改为“虚线”;
(7)单击点E,选择“变换”菜单的“迭代”命令,单击绘图区中的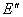 ,不断按键盘上的+号,增加迭代次数,单击“迭代”,如图3.34;
,不断按键盘上的+号,增加迭代次数,单击“迭代”,如图3.34;
(8)画线段EF。

图3.34
[简要步骤]:
(1)新建参数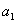 =1,计算
=1,计算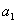 +2,如图3.35;
+2,如图3.35;
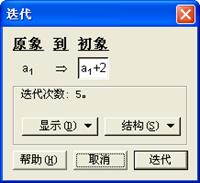
图3.35
(2)新建参数n=10;
(3)选中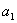 =1和 n=10,按住“shift”,打开“变换”菜单的“带参数的迭代”,打开“迭代”属性对话框;
=1和 n=10,按住“shift”,打开“变换”菜单的“带参数的迭代”,打开“迭代”属性对话框;
(4)单击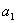 +2=3,然后选择“迭代”,生成如图3.36的图表:
+2=3,然后选择“迭代”,生成如图3.36的图表:

图3.36
迭代的应用
[简要步骤]:
(1)新建参数k=1, 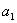 =1,
=1,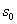 =0,n =6;
=0,n =6;
(2)利用计算工具,算出k+1,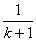 ,
,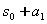 ;
;
(3)选择k=1, =1,
=1, 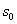 =0,n=6,按住shift,深度迭代,得到如图3.37的数值表:
=0,n=6,按住shift,深度迭代,得到如图3.37的数值表:
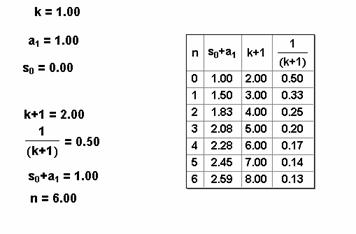
图3.37
【分析】数列的前提条件是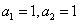 ,因为
,因为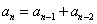 ;所以原像是
;所以原像是 。
。
[简要步骤]:
(1)新建参数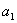 =1,
=1, 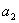 =1,利用“度量”菜单的计算命令,计算
=1,利用“度量”菜单的计算命令,计算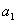 +
+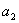 ;
;
(2)右击“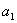 +
+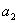 =1”,选择“属性”对话框,把计算结果的标签改为
=1”,选择“属性”对话框,把计算结果的标签改为 ,如图3.38;
,如图3.38;
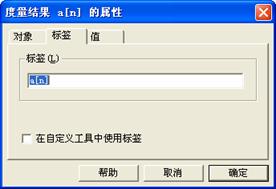
图3.38
(3)新建参数n=8;
(4)依次选择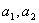 ,n,作深度迭代,单击
,n,作深度迭代,单击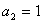 和
和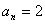 ,得到如下的迭代对话框:
,得到如下的迭代对话框:

图3.39
(5)单击“迭代”,则得到如下的数值表:
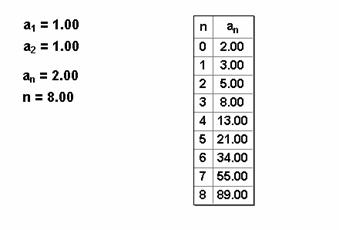
图3.40
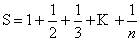 的前n项和。
的前n项和。 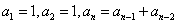 。
。